今回は【ローレンツ曲線】と【ジニ係数】の求め方について簡単に説明していきます。このローレンツ曲線とジニ係数はしばしばセットで登場しますので、
ローレンツ曲線と聞いたらジニ係数を、ジニ係数と聞いたらローレンツ曲線を思い浮かべるようにしてください。
また、ジニ係数は求め方が少しややこしいので注意が必要です。
目次
ローレンツ曲線の導出と性質
まず、ローレンツ曲線から説明していきます。ローレンツ曲線は以下のような方法で導かれます。
ある社会の累積所得比率を縦軸に取り、その社会の人口構成比率を横軸に取った図を想定します。 また、前提条件として、所得が相対的に少ない人から順番に人口を構成すると考えます。
この前提条件がローレンツ曲線の鍵となりますので、確実に理解しておいてください。ここが抜けてしまうと、ローレンツ曲線を説明する際、説得力を欠いてしまいます。
また、ローレンツ曲線の形状の理由もこんがらがってわからなくなってしまうので注意を払ってください。
(例えば、4人の人がいて、それぞれ、300円、200円、100円、400円の所得があるとすれば、所得が100円の人、200円の人、300円の人、400円の人、の順番に並べてグラフを作成するということです。
この例だと、横軸は25%(4人のうちの1人目)、50%(4人のうちの2人目)、75%(4人のうちの3人目)、100%(4人のうち4人目)、
縦軸は、10%(1000分の100)、30%(1000分の300)、60%(1000分の600)、100%(1000分の1000)となります。)
さて、上述の条件より、最初の段階では、人口構成比率が増えても累積所得比率は増加しにくいので、滑らかな曲線になります。
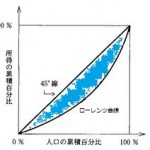
しかし、人口構成比率が100%に近付くにつれ、より多くの所得を持つ人たちで構成されるようになるので、曲線の傾斜は徐々に大きくなります。 そして、この曲線をローレンツ曲線(Lorenz curve)と呼び、以下のように図示されます。
また、人口構成比率が1%増えるにつれ、累積所得比率が常に1%増える状態を考えます。
すると、言うまでもなく原点を通り傾きが1の直線を描くことが出来ます。すると、以下の図のような45度線が登場します。
このとき、図の45度線を均等分布線と呼び、均等分布線が描けるような社会は、完全に平等な状態であると言われています。
なぜこのとき社会が完全に平等な状態といえるかというと、社会全体の所得が均等に配分されているからです。社会全体の構成員の累積増加率と所得の累積増加率が一定ならば、各構成員の所得が一定ということが言えますよね。
例えば、全人口が100人、所得の合計額が100円の時を考えます。このとき、人口の累積百分比が1%増加すると所得の累積百分比が1%増加すると仮定します。すると、人口累積百分比が、1%→2%に動くとき、所得の累積百分比が1%→2%に動きます。
動く前の状態は仮定より累積人口は1人、累積所得1円です。また、2%にそれぞれ動いたとき、累積人口は2人、累積所得は2円です。
初期状態では1人に対して所得1円、1%増大したとき2人に対して合計所得2円なので、それぞれ1円ずつ同等の所得があるということがわかります。
これを帰納的に行えば、100人全員に同額の所得1円が振り分けられてることが示されます。
以上のことから、ローレンツ曲線が45度線と一致するとき、社会は完全に平等な状態であると言われています。
また、ローレンツ曲線がなぜ45度線を下回るような形状を描くのか意味がわからないという方がたまにいらっしゃいます。そんなの分かってるよって方も多くいらっしゃるかもしれませんが、念のため説明をさせて頂きます。
この答えはまさに前提条件にあります。
「所得の少ない人から順番に人口の累積百分比に加算されていく」ということから、45度線を突き抜けてしまう、ということはあり得ません。
例えば、ある人口の累積百分比のとき、所得の累積百分比の方がその時点における人口の累積百分比より大きいと仮定します。
すると、所得の少ない人から順番に並んでいることから、人口の累積百分比がさらに1%増えたとき、所得の累積百分比は前回と同等の伸びかそれ以上伸びることになります。
このことから、これ以降人口の累積百分比が増加していっても45度線より下に位置する可能性はゼロになります。
そして、最終的に人口の累積百分比が100になったとき、所得の累積百分比は100をオーバーしてしまいます。全体の所得の最大値は100であるので、これは明らかに誤り、ということになります。
故に、ローレンツ曲線は45度線を上回ることはありえない、という結論が得られます。
ジニ係数の導出と意味
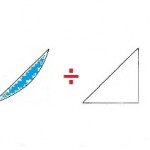
そして、45度線とローレンツ曲線に囲まれる部分を、45度線が成す三角形で除したものこそが、ジニ係数なのです。
やや汚いですが(笑)、45度線とローレンツ曲線に囲まれる部分というのは以下の水色部分です。
そして、この水色の部分を45度線が成す三角形で割ることで求められる数値こそが、ジニ係数である、というわけです。しかし、一般的には、青色部分の面積をすぐに求めることは出来ないので、全体、すなわち45度線が成す三角形から下の領域の面積を引くことで求められます。この部分は後の練習問題で慣れてもらおうかと思います。
最後に、水色部分を三角形で割って出てきた数値がジニ係数というわけです。
以下の図はジニ係数を求める際のイメージ図です。
ジニ係数は社会における所得の分配が平等かどうかを示す指標としてしばしば用いられます。
ジニ係数において最も重要なのは、ジニ係数が1に近い(ローレンツ曲線が45度線から離れている状態)ほど不平等で、ジニ係数が0に近い(ローレンツ曲線が45度線に近い状態)ほど社会は平等であるということです。
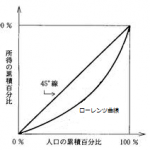
例えば、貧困層と富裕層の格差が大きい社会があるとします。この社会において、ローレンツ曲線は45度線から離れるように描かれます。
なぜなら、ローレンツ曲線の前提条件として、所得水準の低い人々から順に人口が構成されているので、序盤は人口構成比が増加しても累積所得比率はほとんど上がらず、終盤でようやく累積所得比率の上昇幅が大きくなるからです。
そしてこのとき、ローレンツ曲線は45度線から離れるように描かれています。
ローレンツ曲線が45度線から離れるにつれて、45度線とローレンツ曲線に囲まれた部分の面積は大きくなります。
この面積が大きくなると、ジニ係数の数値は1に近付いていきます。
つまり、所得の格差が激しい社会だとジニ係数が1に近付くことから、ジニ係数が高いほど不平等な社会であると言えます。
反対に、ジニ係数が低いほど所得が均等に近い水準で分配されているということが出来るので、比較的平等な状態であると言えます。
*ローレンツ曲線と45度線に囲まれる部分の面積をジニ係数と勘違いする人が多いので、勘違いしないように注意しましょう。
ジニ係数の計算
それでは具体的な数字を使ってジニ係数を求めます。
4つの家計がそれぞれ10万円、20万円、30万円、40万円の所得であるとします。このときのジニ係数を計算します。
まずは、軸についてですが、縦軸には累積所得の百分比率、横軸には人口の累積百分比を取ります。縦軸の累積所得は、各家計の所得の累計額なので、
10万+20万+30万+40万=100万が最大値(合計値)であり、累積所得の百分比率は累積所得が100万円のときに100%(100万/100万=100%)となります。また、累積所得が60万円のときには60%(60万/100万)、30万円のときには30%(30万/100万)、10万円のときには10%(10万/100万)となります。
同様に、横軸の人口の累積百分比については、家計が全部で4なので、1増えるにつれ25%(1人/4人)増えていき、最終的には100%(4人/4人)となります。
この条件から導かれるローレンツ曲線は以下の通りです。
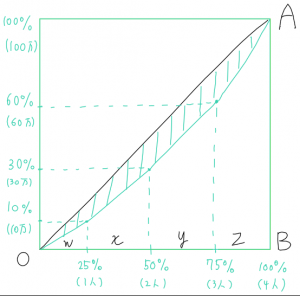
ローレンツ曲線と45度線で囲まれる部分の面積を、45度線が成す三角形の面積で割ったものがジニ係数となるので、
まずは、ローレンツ曲線と45度線で囲まれる部分の面積を計算します。
ただし、直接求めることはできないため、図のようにw、x、y、zの4つの領域に分割して、それらの面積の合計を三角形から控除するという方法で求めます。
wの面積:1×10÷2=5
xの面積:(10+30)×1÷2=20 (台形の面積=(上底+下底)×高さ÷2)
yの面積:(30+60)×1÷2=45
zの面積:(60+100)×1÷2=80
合計=5+20+45+80=150
三角形の面積=4×100=400
よって、ローレンツ曲線と45度線で囲まれる部分の面積は、
400-150=250
以上より、ジニ係数=250/400=0.625となります。
日本のジニ係数と世界のジニ係数の推移
少し古いデータになりますが、1984年から2009年における世界各国のジニ係数の推移は以下の通りです。
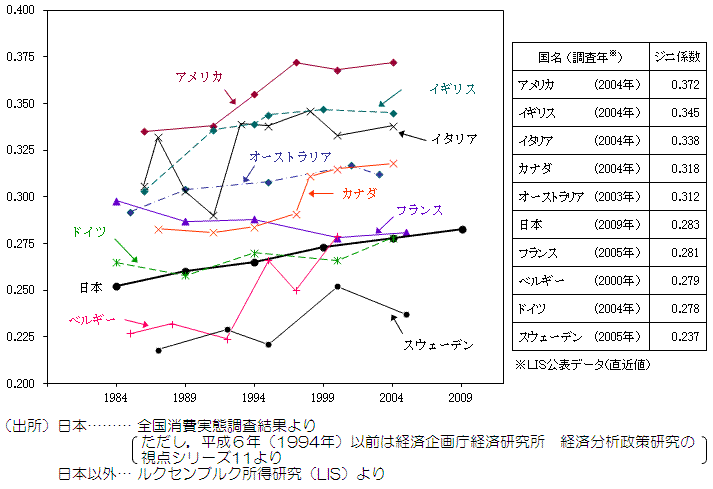
引用元:統計局ホームページ
このグラフを見る限り、世界各国のジニ係数は波がある一方で、日本は30年前からずっとジニ係数が上昇傾向にあることが分かります。日本の経済格差は激しいとメディアでは言われていますが、アメリカやイギリス、イタリアなどの他の先進諸国と比べればまだマシのようです。
日本と産業構造が似ているドイツも日本と同じくらいの水準で推移しており、また2004年にはフランスとも同じような数値を取っています。
そして世界の中で最も税率の高い国の1つとして知られるスウェーデンはやはりかなり低いジニ係数を誇っています。
この30年間で最も高い数値を取っている年である2000年付近でさえ、このグラフにおいて日本の最も低かった時よりも小さい値です。
経済格差の解消は日本の抱える課題の一つではありますが、当面は現状のままだと思います。
というのも、経済が完全に復活しているわけではなく、効果的な政策を打ち出しにくい状態にあるからです。経済格差を是正するには、政府はさらに経済を回復させ、個人消費を増やす等経済を活発にする必要がありそうです。
復習はこちら⇒理解度チェック、ジニ係数の演習問題①、ジニ係数の演習問題②