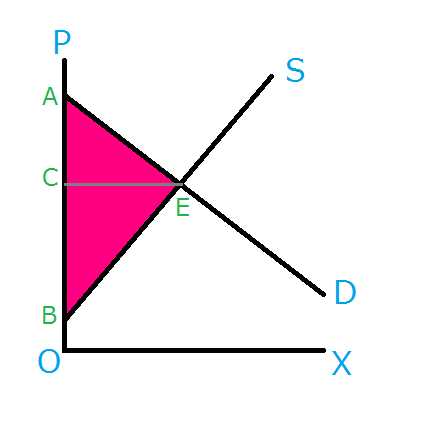余剰分析では、消費者余剰、生産者余剰、社会的余剰をそれぞれ求め、どのような値を取るか、市場の変化や政策の変化によってどのように変化するかを分析します。
ここでは、社会的余剰に関する内容を解説します。
目次
従量税・従価税(消費税)と社会的余剰
社会的余剰とは消費者余剰と生産者余剰とを足し合わせたものであり、社会全体の余剰を表すものであると社会的余剰の記事で説明しました。
しかし、これはあくまでも完全競争市場の場合を前提としています。消費者と生産者以外の第三者、すなわち、政府の存在が無い場合にその等式が成り立つとしているのです。
政府が市場に加わり、財に課税がなされるとすれば、社会的余剰には税収が加えられることになります。しかし、社会的余剰余剰に税収が加えられたとしても、課税がされる前の社会的余剰よりも値が小さくなってしまうことが明らかになっています。
これはいったい何故なのでしょうか。社会的余剰の変化を見ていきましょう。
課税による社会的余剰の変化
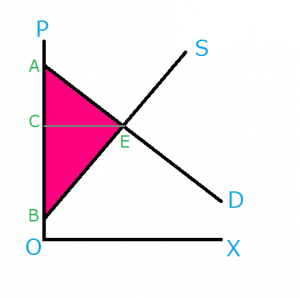
課税される前の状態、すなわち、完全競争市場における社会的余剰は以下の赤紫部分になります。
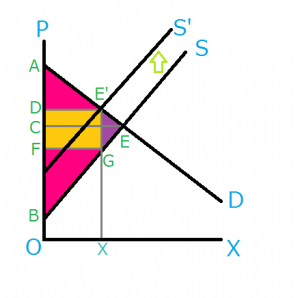
この状態から、課税が行われて供給曲線がSからS’にシフトし、均衡点がEからE’に移ったとします。そのとき、グラフ以下のようになります。
まず、消費者余剰がAE’Dで表せるのは説明するまでもありませんが、消費者にとっては単に価格が上がっただけであり、今まで同様需要曲線と販売価格の直線で囲まれる部分で余剰が計算できるからです。
ここで問題となるのは生産者余剰です。均衡点がE’になったとき、生産者が得られる収入は、ODE’Xとなります。最初に、費用の部分であるOBGXは差し引く必要があります。さらに、E’Gは財1単位当たりの課税額を表し、DE’GFは政府の税収になるので、これも差し引きます。
結果として、生産者余剰はBGFとなります。
最終的に、社会的余剰=消費者余剰+生産者余剰+税収=台形ABGE’となります。
課税前の社会的余剰はABEでしたが、課税が行われることでABGE’となってしまいました。すなわち、紫色の三角形E’GE部分の余剰が失われてしまっているのです。
このように、課税によって社会的余剰が小さくなってしまうことを厚生の損失や死荷重が発生するなどと表現します。
従量税
生産量に応じて課せられる税のことを、従量税と呼びます。例えば、財を1個販売するごとに10円の税金が取られる場合、10円の従量税が課せられていると言えます。
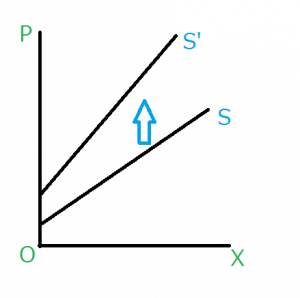
供給曲線がP=X+30で与えられていて、従量税が10課せられたとき、供給曲線はどうなるのでしょうか。
結論から言うと、10だけ上にシフトします。すなわち、P=X+30+10=X+40となります。
供給曲線上のどの点においても、課税がされた場合10だけ費用が増えます。したがって、課税された額をそのまま供給曲線に足せば良いということになります。
補足ではありますが、総費用曲線TCが与えられている場合の処理は少し様相が異なります。TC=X^2+20Xであり、従量税が10課せられたとします。従量税によって生産量1単位につき10の費用が増えると考えられることから、TCに10Xを加えれば従量税を反映した総費用関数を作ることが出来ます。
すなわち、TC=X^2+20X+10X=X^2+30X
少しややこしかったかもしれませんが、供給曲線はあくまで限界費用曲線を表していることを忘れてはなりません。つまり、供給曲線は財を追加1単位作るのに掛かる費用を表す曲線であるので、1単位当たりに一定の課税をする従量税が課せられた場合は、その課税分を足すということになります。
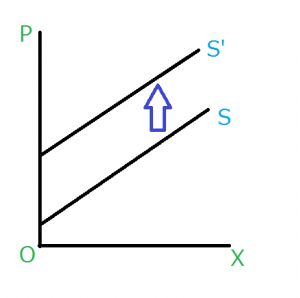
以上のことから、従量税が課されたとき、供給曲線は以下の図のようにシフトします。
従価税(消費税)
価格の大小に応じて課税される額が変化する税を従価税と呼びます。従量税のもっとも代表的な例は消費税です。消費税の金額は、財の価格が大きいほどそれに応じて金額も大きくなりますよね。
現行の消費税である8%で供給曲線がどう変化するか考えます。
このとき、P=X+30の供給曲線があるとします。P=X+30より、価格=(X+30)で表されます。そしてこの(X+30)に8%の価格が上乗せされるので、1.08を掛けます。すると、
P=1.08(X+30)
=1.08X+32.4
となり、これが求める供給曲線です。
ご覧の通り、従価税が課された場合は、上にシフトするだけでなく、曲線の傾きも変化します。従量税の場合は単に上にシフトするだけでしたよね。
従価税は供給曲線の傾きさえも変えてしまうということに注意しましょう。
以上ことから、従価税が課された場合の供給曲線は以下のようになります。
従量税(死荷重)の練習問題
需要曲線がP=-X+74,供給曲線がP=X+10で与えられている財の市場があるとする。この財に対して10%の従価税が課せられたとき、生産者余剰および発生する死荷重の値を求めよ。
解)
まずは、課税前の均衡点を計算します。P=-X+74,P=X+10の2式を連立して、
P=42,X=32
が得られます。
続いて、課税後の均衡点を考えます。最初に課税後の供給曲線を導出します。10%の従量税が課されているので、P=1.1(X+10)=1.1X+11
次に、この課税後の供給曲線と需要曲線を連立して均衡点を求めます。すると、
P=44,X=30
が求まります。
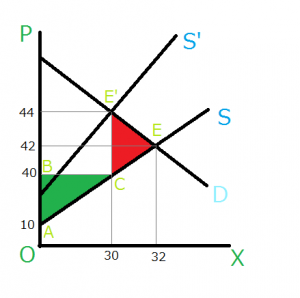
また、この均衡点から、元の供給曲線へ向かっておろした垂線の交点を求めます。X=30のとき、P=30+10=40となります。この点をCとします。
すると、生産者余剰は図の緑色の部分、すなわち、三角形ABCの面積であるから、
生産者余剰=1/2×30×30=450
死荷重は図の赤色の部分、すなわち、三角形EE’Cの面積であるから、
死荷重=1/2×(44-40)×(32-30)=4
となります。