今回は、所得効果と代替効果をどのように測るかを説明していきます。所得効果と代替効果を分割して測る代表的な方法には、スルツキー分解というものがあります。このスルツキー分解とはいったいどのような手法なのでしょうか。慣れるまでは少し厄介かもしれませんが、順を追って確認していきましょう。
目次
スルツキー分解
スルツキー分解とは、価格の変化による最適消費点の変化(全部効果)を所得効果と代替効果に分け、それぞれの効果を明確にする方法です。スルツキー分解では価格の変化前後のグラフを用いて、所得効果と代替効果を求めます。
すなわち、グラフを使って最適消費点の移動に着目し、その移動の性質によってそれぞれ所得効果と代替効果に分けて分析しているのです。そこで、所得効果と代替効果を判別するためのキーワードを挙げます。
- 無差別曲線上の点の移動は代替効果
- 予算線上の点の移動は所得効果
- 代替効果が先、所得効果が後
単純化され過ぎて分かりにくいかもしれませんが、この記事を読み終える頃にはこのキーワードの意味が明瞭に分かるはずです。
それでは、X,Yの2財があり、Xの価格が下落したときのスルツキー分解を行っていきます。
なお、上級財や下級財、ギッフェン財については、『所得効果と代替効果①~上級財(正常財)、下級財(劣等財)、ギッフェン財の分析 』を参照して下さい。
X財の価格が下落したとき(X財:上級財)
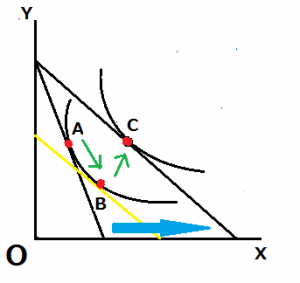
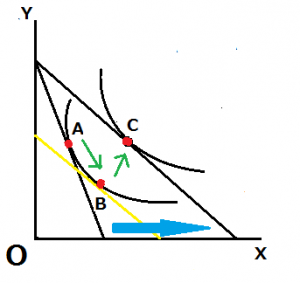
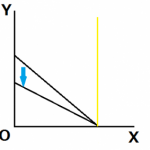
当初、A点で消費量が均衡、すなわち最適消費点だったとしましょう。X財の価格が下落し、予算線は水色の矢印方向にシフトし、最適消費点はC点になったとします。このように予算線がシフトする理由を説明する際、以下の2つの方法で示すことが出来ます。
1つ目は予算線の傾きに着目することです。予算線の傾きは-Px/Pyで表され、分子のPxが小さくなれば当然傾きは小さくなるので緩やかな予算線になることが想定されます。
2つ目はX軸切片に着目することです。X軸と予算線の交点は0=-(Px/Py)X+M/Pyより、X=M/Pxで表されます。分母であるPxの値が小さくなるとこのX軸切片が大きくなるので、右にシフトするということが分かります。
A点からC点への移動が全部効果であり、X財,Y財共に数量が増えていることが見て取れますよね。しかし、所得効果と代替効果がそれぞれどの程度影響を与えているかがわかりません。
そこで、価格の変化により新しく形成された予算制約線と同じ傾きで当初の無差別曲線と接する補助線を描きます。これがスルツキー分解の肝となるので、必ずこの部分を明確に暗記して下さい。
この補助線と無差別曲線の接点が代替効果を反映した最適消費点となります。最初に掲げたポイント通り、最初に代替効果から表れています。
さらに、B点からC点への移動が、所得効果を表しています。予算制約線の補助線上の点から、新たな予算制約線上の点へと平行移動し、所得の増減が消費量に影響を与えているという意味で、この効果は所得効果と呼ばれています。
また、この例の場合、価格が下落した時に代替効果及び所得効果により消費量が増大しているのでX財は上級財であるということがわかります。
X財の価格が上昇したとき(ギッフェン財)
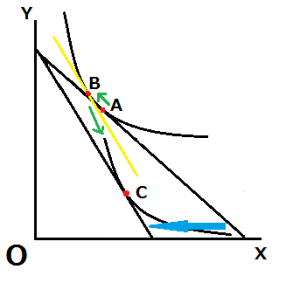
同様に、当初A点で最適消費点であるとします。そして、X財の価格が上昇し、予算線は水色の矢印方向にシフトし、最適消費点はC点に移動したとします。価格の上昇により予算線がこのようにシフトする理由は価格が下落したときと同じものなので、ここでは割愛します。
A点からC点への移動が全部効果を表しており、図よりX財の数量は増大し、Y財の数量は減少していることがわかります。X財は自身の価格の下落により数量が増大していることから、X財はギッフェン財ということが明らかですよね。
また、ギッフェン財ならば、価格が上昇したとき、所得効果はプラス、代替効果はマイナスとなるはずです。そこで、価格の変化により新しく形成された予算制約線と同じ傾きで当初の無差別曲線と接する補助線を描き、所得効果と代替効果の影響を見ていきましょう。
この補助線と無差別曲線の接点と当初の最適消費点の差が代替効果を反映した最適消費点となります。左上に移動していることから、X財は減少し、Y財は増加していることがわかります。
さらに、B点からC点への移動が、所得効果を表しています。所得効果により、Y財の数量は減少し、X財の数量は増加しています。
最終的に、価格が下落した際、代替効果がマイナスで所得効果がプラスだということが分かりました。このことから、この財は下級財であることが分かります。また、所得効果が代替効果を上回り結局数量が増大していることから、ギッフェン財であると判断することが出来ます。
復習はこちら⇒理解度チェック