問題
需要曲線がD=100-2P、供給曲線がS=-20+2Pで与えられている。
この場合における生産者余剰はいくらになるか。
解説
需要曲線、供給曲線の式をそれぞれP=の式に変形します。
すると、需要曲線はP=50-D/2、供給曲線はP=S/2+10となります。
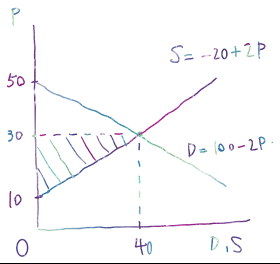
これらを図示すると以下のようになります。
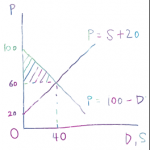
P=50-D/2,P=S/2+10を連立すると、P=30,D=S=40となることから、交点は上記の位置になります。斜線部分の三角形の面積が生産者余剰なので、この面積を求めます。
底辺をP軸側の部分、高さをD,S軸側の部分とみると、
斜線部分の面積=底辺×高さ÷2=(30-10)×40÷2=400