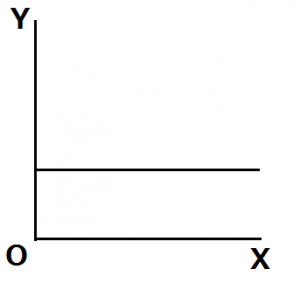無差別曲線と一口言ってもその種類は様々です。一般的には、反比例のグラフになりますが、どんな財の組み合わせを選ぶかによってその形状は異なります。
ここでは、どのような無差別曲線があるのかということを紹介していきます。
一般の無差別曲線については、『予算制約線と無差別曲線』をご覧ください。
目次
特殊な形の無差別曲線
一つ前で紹介した記事では一般的な無差別曲線について確認しました。すなわち、最も取り上げられる無差別曲線の説明をしました。しかし、あくまで一般的な形状であってあれがすべてではありません。
今回は前回紹介したような一般的な無差別曲線ではなく、特殊な形をした無差別曲線について論じていきます。
1. L字型の無差別曲線
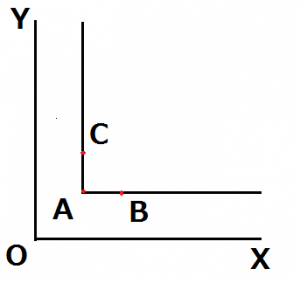
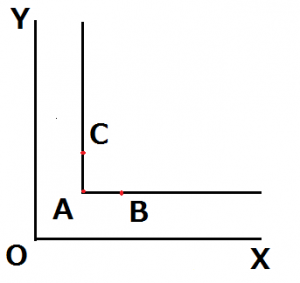
消費者が消費する2財が補完財であるとき、無差別曲線はL字型で描かれます。補完財とは、2財が同数(もしくは同じ比率)だけあって初めて役に立つものであり、片方の財の数量が変わらない状態でもう一方の財の数量を増やしても効用は一定となります。
グラフを図示すると以下のようになります。
X財を右足の靴、Y財を左足の靴とします。X,Yが共に同数でありA点に位置するとします。このとき、Yを保ったままいくらXを増やしたとしても、効用に変化を及ぼしません。
何故なら、Xだけ増えてもセットとなるYが足りないため、意味がないからです。同様に、Xを保ったままYを増やしても意味はありません。
2. 凹型の無差別曲線
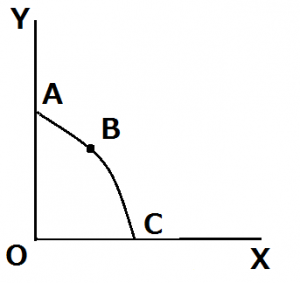
消費者がそれぞれの2つの財を別に消費する方を好む場合、無差別曲線は原点に対して凹型の無差別曲線を描きます。
X財をラーメン、Y財をコーヒーとします。また、消費者はラーメンとコーヒーはどちらも好きですが、同時に消費するのは気が進まないとします。
このとき、どちらか一方を消費した方が高い効用を得られます。また、仮にコーヒーだけ消費している状態Aからラーメンを一単位増やしてコーヒーを減らすとします。このとき、ラーメンを増やしたときの効用はそれほど大きくないので、少量だけコーヒーを減少させ、B点へと移ります。
さらに、B点から再びラーメンを増やすと、同時に消費することを望まない消費者にとって、ラーメンだけ食べることの方が満足を得られるので、それに合わせて効用が一定になるようにコーヒーの量を減らします。
ここで、この消費者はより多くのラーメンを消費することでより多くの効用を得られるので、その分コーヒーから得られる効用を減らさなければなりません。
つまり、ある1つの無差別曲線を考えるとき、ラーメンの消費を増やすにつれて、コーヒーの消費をより多く減少させなければなりません。そして、最終的にはもうラーメンだけでよくなってC点へと移ります。
このとき、片方の財を増やすことによるもう一方の財の数量の減少幅が徐々に大きくなっていっています。すなわち、限界代替率が逓増しています。
凸型は限界代替率逓減と言われているのに対して、凹型は限界代替率逓増であると言われています。
3. 右下がりの直線の無差別曲線
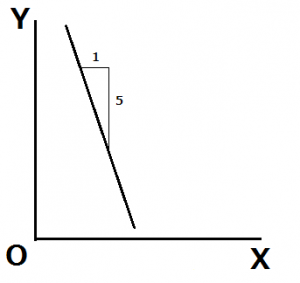
X,Yの2財が完全代替財、すなわち、完全な代替関係であるとき、無差別曲線は右下がりの直線となります。つまり、XとYの個数に関係なく、交換比率が常に一定のものの組み合わせのときに、以下のような右下がりの直線が描けるというわけです。
Xを500円玉、Yを100円玉とします。Xが1増えたとき、効用を保ちつつYを変化させるとすると、Yは当然5減らせば良いですよね。
Xが1増えるというのは500円増えるということ、Yが5減るというのはすなわち100×5=500で500円減るということになるので、結局全体の金額は変わっておらず、効用は変化しません。
つまり、この直線上の効用は等しく、直線の無差別曲線であると言えます。
4. 水平な無差別曲線
横軸にとった財が効用に影響を及ぼさないとき、水平な無差別曲線が描かれます。
例えば、りんごをX、みかんをYとし、消費者はみかんだけが好きでりんごは食べても食べなくてもどっちでもいいと考えているとします。みかんの消費量が増えないとき、りんごをいくら食べたとしても効用は変化しません。すなわち、消費者の効用はみかんの数量によって決まり、その無差別曲線は水平になります。
5.垂直な無差別曲線
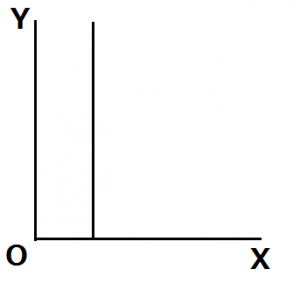
縦軸にとった財が消費者の効用に影響を及ぼさないとき、垂直な無差別曲線が描かれます。
例えば、りんごをX、みかんをYとし、消費者はりんごだけが好きでみかんは食べても食べなくてもどっちでもいいと考えているとします。りんごの消費量が増えないとき、みかんをいくら食べたとしても効用は変化しません。
すなわち、消費者の効用はりんごの数量によって決まり、その無差別曲線は垂直になります。
6. 円型の無差別曲線
2財において効用を最大にする数量の組み合わせが一意的に決められる場合、円型の無差別曲線を描くことができます。
Xをケーキ、Yを紅茶とします。また、ある消費者はケーキ3個、紅茶3杯の組み合わせが一番幸せだと感じるとしましょう。この時上のグラフの円の中心で効用が最大になっているとすることが出来ます。
円の中心から離れた状態、例えば、ケーキ2個、紅茶4杯やケーキ3個紅茶4杯では最適な数量のときよりも得られる効用が小さくなります。したがって、この円型の無差別曲線の場合、円の中心が効用の最大を達成することが出来る点ということになります。
復習はこちら⇒理解度チェック
また、特殊な無差別曲線の最適消費点については、『特殊な無差別曲線と最適消費点』で解説していますので、理解度チェックをした後ご覧ください。