今回は代替財、補完財、独立財について説明します。それぞれの財がどのような性質を持つ財であるのかを確認していきます。名称からある程度推測できると思って油断していると度忘れしてしまう可能性などもあるので、きちんと理解しなければなりません。
また、スルツキー分解を行って所得効果や代替効果についても見ていくので、この辺の理解があやふやな方は『所得効果と代替効果②~スルツキー分解~』を参照して下さい。
目次
代替財
代替財とは、ある2つの財について、片方の財の価格が変化すれば、もう一方の財の需要量がその変化と同じ符号で変化するという関係にあるものです。
すなわち、片方の財の価格が上昇すればもう一方の財の需要量が増大し、片方の財の価格が下落すればもう一方の財の需要量が減少するという関係にある財のことです。
例えば、米とパンの関係が挙げられます。何らかの理由でおにぎりの価格が100円上がったとします。すると、朝ごはんにおにぎりではなくパンを選択する人が増えます。結果として、パンの消費量はおにぎりの価格が上昇する前よりも増大します。
一方で、おにぎりの価格が100円下がった時を考えます。この時、安くおにぎりを買うことが出来るので、朝食としてパンを選ぶ人が少なくなります。結果として、パンの需要量はおにぎりの価格が下落する前よりも減少しますよね。
このように、片方の財の価格の上昇(下落)が、もう一方の財の需要を増大(減少)させる関係にある2つの財を指します。
この性質から、代替財は需要の交差弾力性がプラスであることがわかります。
さらに、代替財は粗代替財と完全代替財(純粋代替財)に分けることが出来ます。
完全代替財
ある財とその代替財の効用比率が一定(限界代替率が一定)のとき、その2財の組み合わせを完全代替財と言います。効用の比率が一定ということは、無差別曲線の限界代替率が一定、すなわち、無差別曲線が線形であることを示します。無差別曲線が線形となることから、最適消費点はコーナー解となります。
また、スルツキー分解を行って完全代替財の所得効果、代替効果を確認していきましょう。
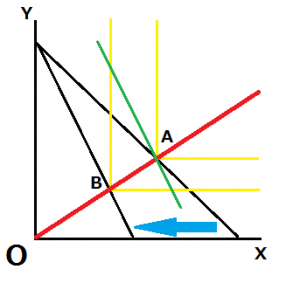
黒い線分を予算制約線、黄色の線分を無差別曲線とし、当初A点で最適な消費水準であったとします。今、X財の価格が下落して水色の矢印方向に予算制約線がシフトしたとします。この時、無差別曲線の形状より点Cが最適消費点となります。
ここで、スルツキー分解を行います。スルツキー分解では、新たに形成された予算制約線と同じ傾きで、当初の無差別曲線の効用を達成するような補助線を引くことから、図の緑の線分が描かれます。
代替効果は当初の最適消費点から補助線と当初の無差別曲線における最適消費点への移動で表せることから、A点からB点への移動が代替効果であることがわかります。また、B点からC点への移動が所得効果を表します。
価格が下落した際に代替効果によりその財の消費量が格段に減少することより、完全代替財は極めて代替効果が強いと言えます。
粗代替財
完全代替財以外の代替財を粗代替財と呼びます。厳密に言うと、片方の財の価格の変化がもう一方の財の数量に同じ方向の影響を及ぼし、かつ得られる効用が常に一定の比率ではない2財であると言えます。
一般的に、代替財と呼ばれる財に当てはまるのは完全代替財ではなく、この粗代替財です。
補完財
補完財とは、ある2つの財について、片方の財の価格が変化すると、他方の財の需要量に逆方向の影響が及ぶという関係にあるものです。すなわち、片方の財の価格が上昇すれば他方の財の需要量が上昇し、片方の財の価格が下落すれば他方の財の需要量が減少するという関係にある財のことです。
例えば、ゲーム機とゲームソフトの関係について考えます。ゲーム機の価格が2倍になったとします。
すると当然、ゲーム機に対する需要が下がります。さらに、ゲーム機の需要量が小さくなれば、ゲームソフトの需要量も同様に小さくなります。何故なら、ゲームソフトはゲーム機を持っていなければ利用することができないからです。結果としてゲームソフトの需要が下がります。
逆に、ゲームソフトの価格が2倍になるとどうでしょうか。消費者にとって、ゲーム機を買ったとしてもゲームソフトを買わなければゲーム機を買った意味がありません。したがって、消費者はゲーム機を購入する前に、ゲームソフトの価格も考慮します。
そこで、ゲームソフトの価格が高くなってしまうと、ゲーム機を購入する意欲が低減するので、ゲーム機への需要が下がります。
このように、片方の財の価格の上昇が、もう一方の財の需要を減少させる関係にある2つの財を指します。
この性質から、補完財は需要の交差弾力性がマイナスであることがわかります。
さらに、補完財は完全補完財と粗補完財に分けることが出来ます。
完全補完財
ある2つの財について、両方の財の数量が一定の比率で両方とも増加しなければ効用を高めることが出来ないような財を完全補完財と言います。例えば、靴を例として考えてみましょう。靴は両足で1セットになるので、片方の足だけ数量が増えても意味がありませんよね。
両足セットの靴を3つと右足の靴を5つ持っている場合と、両足セットの靴を3つと左足の靴を2つもっている場合ではどちらも得られる効用は同じなのは明らかです。何故なら、片足だけでは使用できないため、効用に影響は及ばないからです。
さらに、完全補完財の場合、L字型の無差別曲線が描かれます。L字型の無差別曲線はレオンチェフ型の効用関数とも呼ばれます。
スルツキー分解を行って、L字型の無差別曲線を描く完全代替財の所得効果と代替効果について見ていきましょう。
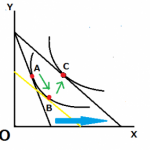
黒い線分を予算制約線、黄色い線分を無差別曲線とし、当初点Aで最適消費点だったとします。ここで、X財の価格下落により、水色の矢印方向に予算制約線がシフトし、B点で新たな最適消費点となったときのことを考えます。
まず、スルツキー分解を行うために、価格変化後の予算制約線と平行で、当初の無差別曲線の効用を達成する線分を引きます。図でいうと、緑の線分がそれを表します。
代替効果は、当初の最適消費点から、補助線と当初の無差別曲線における最適消費点への移動で表せます。この場合、当初の最適消費点と、補助線と当初の無差別曲線の最適消費点が一致することから、代替効果は発生しないということになります。また、所得効果はA点からB点への移動で表されています。
つまるところ、完全補完財の場合、代替効果がゼロであり、所得効果しか発生しないことが分かります。
粗補完財
補完財の中で、完全補完財以外の財を粗補完財と呼びます。補完財の定義と同様であると考えて頂ければ良いでしょう。
独立財
片方の財の価格の変化がもう一方の財の消費量に何も影響を及ぼさないものです。
例えば、傘とおにぎりを考えましょう。傘の価格が1000円上がったとします。すると、おにぎりの消費量はどのように変化するでしょうか。もちろん、財の性質が全く異なる上に関連性がないので、全く影響が及ばないのは簡単に想像がつきますよね。
このように、他の財に対して影響力を持たない財を独立財と呼びます。
この性質から、独立財の需要の交差弾力性は0であることがわかります。
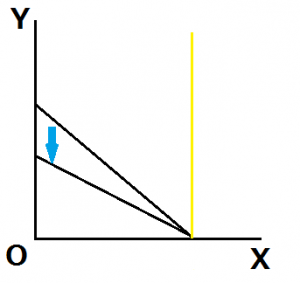
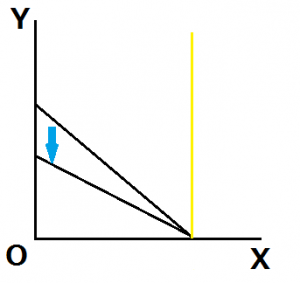
また、独立財の1つの例として考えられる図を見てみましょう。
黒い線分を予算制約線、黄色い線分を無差別曲線とし、Y財の価格が下落したとします。このとき、水色の矢印方向に予算制約線がシフトします。しかし、無差別曲線の形状から、最適消費点は移動せずにとどまります。この時、代替効果及び所得効果は明らかに発生していません。
このように、価格が変化した際に所得効果、代替効果が発生しない財の組み合わせを独立財と呼びます。
無差別曲線の理解に不安がある方は、『特殊な形状の無差別曲線』及び『特殊な無差別曲線と最適消費点』を読んで頂ければ解決すると思います。
復習はこちら⇒理解度チェック