マクロ経済学の代表的なグラフであるIS曲線とLM曲線。今回はIS曲線について、グラフや計算方法などを簡単に説明します。
目次
IS曲線とは
IS曲線とは、投資(Investment)と貯蓄(Saving)が等しいときの利子率と国民所得の関係を表す曲線で、一般的に右下がりの曲線になります。投資と貯蓄が等しいとき、財市場の需要と供給も均衡しているので、財市場の需給均衡を表す曲線であるとも言えます。
財市場の均衡から、投資と貯蓄の関係を見てみます。財市場の均衡はY=C+Iで求められ、左辺は財市場の供給で右辺は需要を表します。さらに、貯蓄Sは所得Yから消費を差し引いたものであるので、S=Y-Cとなります。これより、
Y=C+I,S=Y-Cを連立して、
S=(C+I)-C ⇔ S=I ⇔ I=S
と求めることが出来ます。
投資IはI=-ar+I'(a:定数、I’:独立投資)と表され、利子を変数とする関数になります。利子率rの符号がマイナスであるので、利子率が高いほど投資が小さくなり、利子率が低いほど投資が活発になることが分かります。
これは、実際の経済に照らし合わせて考えてみたらさらに納得がいくかもしれません。多くの企業は設備投資をして事業を拡大する際、銀行からその資金を借り入れます。借り入れた資金で新たな設備を購入して稼働させ、それから得られるキャッシュフローを元に借入金を返済します。
そこで問題となるのが銀行の利子です。例えば、2億円を年利5%で借り入れた場合、年間で1000万円の利子を支払わなければなりません。しかも、設備投資など額が大きい借入金の場合、返済は中長期になることが多いので、さらに多額の利息がのしかかります。
そのため、企業にとって、利子率というのは投資をするかどうかの最も重要な材料の1つであると言えます。そして、利子率が高ければ投資を控え、利子率が低ければ積極的に投資を行おうとするのです。つまり、利子率が低いほど国民所得Yが大きくなると考えられます。
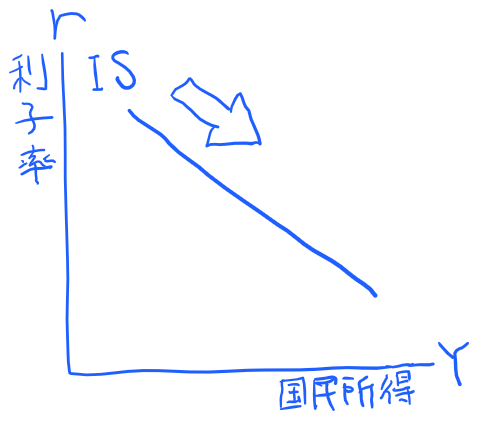
以上を踏まえて、利子率rを縦軸、国民所得Yを横軸に取り、IS曲線を図示すると以下のようになります。
また、IS曲線が右下がりになる理由を違う視点から見てみます。
IS曲線は財市場の需要と供給が均衡しているときのYとrの組み合わせです。したがって、そのIS曲線上に無い点については、需要と供給が均衡していないと考えられます。すなわち、超過需要または超過供給が発生していると判断できます。
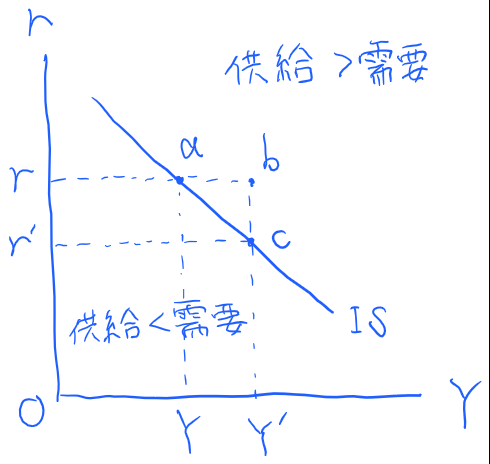
IS曲線より上にある部分については、超過供給が発生しており、IS曲線より下にある部分については、超過需要が発生しています。
IS曲線上の点は財市場の需要と供給が均衡しているので、点aにおいて市場は均衡しています。ここで、点aに関して、国民所得Yが増大してYからY’になったとします。このとき、点aは右に移動して点bへと移ります。
点aでは需要と供給が等量、すなわち、どちらもYで均衡していました。しかし、点bにおいては、需要はYのまま、供給がY’になってしまっています。つまり、需要より供給が大きい超過供給の状態にあります。
もう一度需給が均衡した状態に戻るためには、供給に等しくなるよう需要を高める必要があります。利子率rが下落し利子率r’の場合において、需給の均衡が再度達成されるとすると、図の点cがその条件を満たす点となります。
そして、需要と供給が均衡する点aと点cを結んでできる曲線がIS曲線です。
また、IS曲線の形状は、等式からも導くことが出来ます。
財市場の需要と供給の均衡式をY=C+I+Gとします。
これに、消費関数C=cY+c’、投資関数I=-ar+I’を代入すると、
Y=cY+c’-ar+I’+G
IS曲線は利子と国民所得の関係を表すので、r=の形にします。
すると、
⇔ ar=-Y+cY+c’+I’+G
⇔ ar=-(1-c)Y+c’+I’+G
⇔ r = -(1-c)Y/a+(c’+I’+G)/a
となり、傾きが-(1-c)/aという負の値を取ることから、右下がりの曲線になることが分かります。
また、切片は(c’+I’+G)/aです。
この式を理解して覚えておけば、IS曲線のシフトや形状の変化に関する問題は容易に解けるのではないかと思います。
IS曲線のシフト
シフトする例として最も代表的なものは、政府支出の増減です。
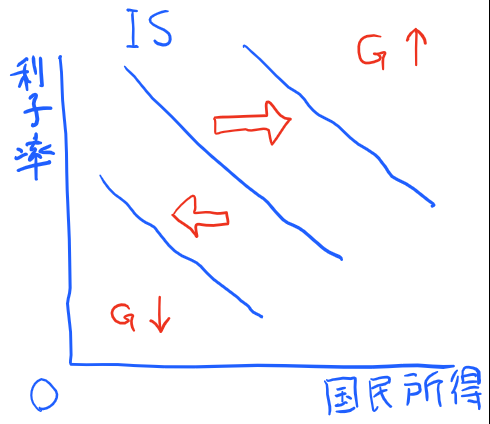
国が財政政策を行うことで政府支出を増やした場合、IS曲線は右にシフトします。一方、国が政府支出を減らした場合には、IS曲線は左にシフトします。
このシフトの原理はIS曲線の式から考えると容易に理解できます。IS曲線の式は
r = -(1-c)Y/a+(c’+I’+G)/a
で表され、切片は(c’+I’+G)/aです。
すなわち、Gが増加すれば切片は大きくなるため曲線は上に動き、Gが減少すれば切片が小さくなるため曲線は下に動きます。
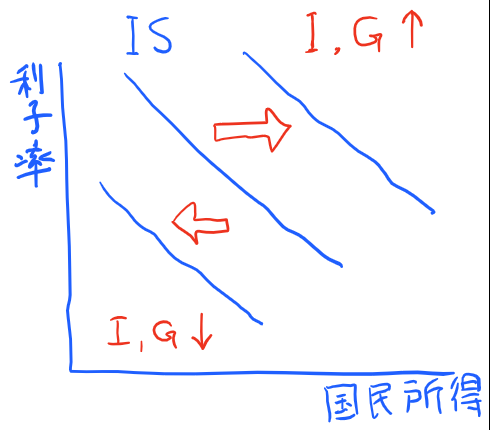
このように、政府支出の増加、投資の増加はIS曲線を上にシフトさせ、反対に、政府支出の減少、投資の減少は下にシフトさせる働きがあります。
特殊なIS曲線の形状
IS曲線は一般的には右下がりになりますが、垂直になったり、水平になったりする場合があります。これらの場合について考察していきます。
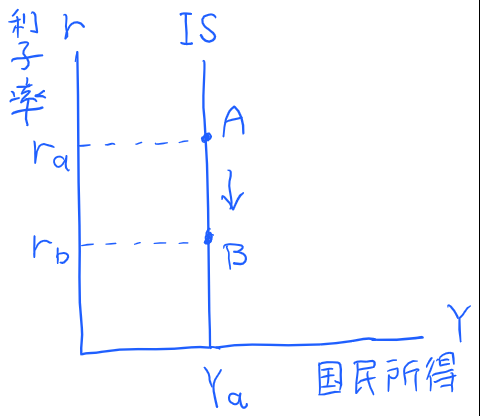
まずはIS曲線が垂直になる場合のIS曲線の性質を見てみましょう。IS曲線が垂直となるときのグラフは以下の通りです。
このとき、国民所得は利子率の影響を一切受けません。図のように、利子率がraからrbに下がったとします。この場合、IS曲線上の点Aは点Bへと移動します。しかし、単に点は真下に動いただけであって、国民所得はYaのままで変化しません。利子がいくら高くなろうと低くなろうと、国民所得には何の影響も及ばないのです。
このような状態は、投資が利子に対して完全に非弾力的である状態と言われます。ここで、非弾力的とは、全く影響を及ぼさないことを表します。すなわち、投資の利子弾力性がゼロであるともいえます。
これで、IS曲線が垂直なときの利子と国民所得の関係は分かりました。次に、IS曲線が垂直になるのはどういうときかを、IS曲線の式から考えます。
IS曲線の式は
r = -(1-c)Y/a+(c’+I’+G)/a
で表されます。
垂直になるということは、傾きが限りなく大きくなるということなので(傾きが1の直線よりも傾きが100の直線の方が垂直に近いですよね。)、傾きである-(1-c)/aが無限大に近付けば良いということになります。
限界消費性向cは0≦c<1なので、分子の-(1-c)は大きな値を取ることは出来ません。そこで分母に着目すると、分母であるaが限りなく小さいとき、傾きが無限大へと近付きます。このことから、-(1-c)がそれほど小さくなく、投資関数の定数aが非常に小さければ、IS曲線が垂直になることが分かります。(ちなみに、投資関数I=-ar+I’で表されることから、定数aが0に近ければ、投資関数も利子の影響を受けないこととなります。)
同様に、IS曲線が水平となる場合のIS曲線の性質を見ていきます。IS曲線が水平となるとき、IS曲線のグラフは以下のようになります。
IS曲線が水平なとき、投資の利子弾力性が無限大、投資が利子に対して完全に弾力的などと言われます。ちょっとこれは分かりにくいんですが、IS曲線がほんの少しだけ右下に傾いていると考えてみてください。このとき、利子率が下がれば、国民所得は大きく増えますよね?
すなわち、IS曲線が水平に近付けば近付くほど、利子の影響を強く受けます。このことから、IS曲線が水平のときは、投資の利子弾力性が無限大などと表現されます。



コメント
すごくわかりやすい
勉強になりました
ありがとうございます。
お役に立てて嬉しいです。
色々な動画や参考書でもわからなかったのが、一発でわかりました。
素晴らしい!!
感謝しております。
ありがとうございます!お役に立てて良かったです^^
S曲線は、( A )の均衡を維持することのできる利子率と国民所得の組み合わせを示すものである。総需要が消費と投資のみで成り立っているとすると、利子率が低下した場合、( B )が増加する。一方、需要と供給が均衡するためには、( B )と量的に等しい( C )も増加しなければならない。したがって、利子率が低下した場合、国民所得は( D )。
≪選択肢≫
「生産物市場」、「貨幣市場」、「労働市場」、「消費」、「投資」、「貯蓄」、「増加する」、「減少する」