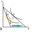特殊な無差別曲線と最適消費点

ｅｃｏｎ

10年前

一般的な無差別曲線では、無差別曲線と予算線が接するところで消費者の効用が最大化され、最適な消費点であることは以前の記事で確認しました。

今回は、特殊な無差別曲線の時、どの点で最適消費点が達成され、効用が最大化されるかを論じていきます。

さて、本題に入る前に、無差別曲線の性質は何だったでしょうか。

まだあやふやであるという方のために、再度掲示しておきます。

無差別曲線については、『予算制約線と無差別曲線』、『特殊な形状の無差別曲線』でも解説しています。

特殊な無差別曲線の最適消費点

前回の記事で紹介したように、無差別曲線は様々な形状が存在します。その形状によって、最適消費点の定め方が異なります。したがって、それぞれの場合について、どのように最適消費点が決められているかを見ていきましょう。

以下、予算制約線を黒色の線分、効用最大化を満たさない時の無差別曲線を青色の線、効用最大化を満たす無差別曲線を赤色の線で示しています。

L字型の無差別曲線の場合、予算線と接するときに効用が最大化されます。すなわち、一般的な無差別曲線の効用最大化と同じ条件です。上図では赤色の線分で示されています。

例えば、下部にある青色の線分が無差別曲線のとき、この線分の一部は予算線の領域に含まれていますよね。これはつまり、まだ右上に動いてより高い効用を得る余裕があるということです。

一方、上部にある青色の線分はどうでしょうか。この線分は下の何れの線分よりも効用が高く、消費者にとってはこの一番上位に位置する線分の効用を得ることが望ましいでしょう。

しかし、この線分は予算線よりも遥かに上に位置します。従って、いくら消費者がこのような効用を得ようとしても、所得が足りないがためにこの効用を達成することは到底不可能なのです。

そして、これより下に位置する無差別曲線で予算の範囲内にあるものを模索することになります。最終的に、赤色の線分の位置で折り合いがつくというわけです。

続いて、凹型の無差別曲線の最適消費点についてです。少し作図が下手ですがご容赦下さい笑

凹型の無差別曲線の注意点は、予算線と接する点が最適消費点ではないことです。今までの流れだと、どんな無差別曲線でも基本的に接する点で最適な消費水準となっていたんですが、今回は違います。

必ずしも無差別曲線と予算線が接する点が最適消費点ではないということを強く認識しておいて頂ければ良いかと思います。

まず、一番下の青色の無差別曲線を見てみましょう。この線分は予算線と接しており、少しこの手の問題に慣れている人なら一見効用が最大化されていると勘違いしてしまいがちです。しかし、この無差別曲線はあくまで予算線の領域の中にいます。

つまり、無差別曲線を右上にシフトする余地があり、より高い効用を得ることが出来るということです。予算線の範囲内で無差別曲線を右上にシフトさせていき、最終的に予算線の端点で最適消費点を得られます。また、このように解が端となる点をコーナー均衡といいます。

このグラフでは、予算線の両端で最適消費点となっていますが、一般的には、予算線の右端か最上部で最適消費点となります。

これも少し紛らわしいんですが、凹型の無差別曲線の場合と同様、無差別曲線が予算線と端点で交わるときに効用の最大化が達成されます。説明がくどくなってしまうのでこれほどにしておきますが、例えば、左端の青色の無差別曲線は、予算線の領域内にあり、右にシフトする余裕がありますよね。

そして、予算線の領域から出ないように無差別曲線を右に移動させて交点を求めれば、そこが最適消費点となります。

垂直な直線の無差別曲線の場合も、予算線の端で最適消費点となる。理由は右下がりの直線の無差別曲線の場合と同じです。ただし、垂直な無差別曲線はその形状ゆえ、必ず無差別曲線の右端で最適消費点になります。

垂直な直線の無差別曲線の場合も水平な無差別曲線の場合と考え方は同じです。しかし、垂直な無差別曲線と違って、予算線の上端で最適消費点となります。理由はここまで読んで頂いた皆様ならすぐにお分かりでしょう。

最後に円型の無差別曲線の最適消費点です。円型の無差別曲線は本当に特殊で、この場合だけ必ずしも予算線上に最適消費点があるとは限らないということになります。確認ですが、円型の無差別曲線の性質は、その円の中心に近付くほど効用が大きく、円の中心で最大の効用を表す、ということでしたよね。

まず、予算線が青色の直線の場合を考えましょう。このとき、内円の無差別曲線のほうが外円の無差別曲線が大きいことから、最適消費点は青色の予算線と内円の無差別曲線の接点となります。

一方、予算線が赤色の直線の場合、効用が最大である円の中心を予算線が内包していますよね。

したがって、この点が円型の無差別曲線の最適消費点となるわけです。